Ac Voltage Source
In this example we build an AC voltage source using a Twist and supply a resistor.
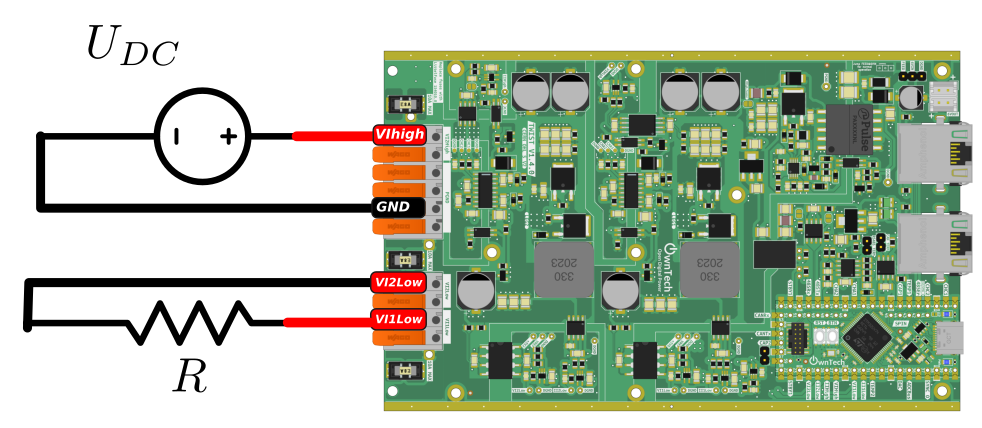
The parameters are:
- \(U_{DC} = 40 V\)
- \(R_{LOAD} = 30 \Omega\).
Software overview
Import libraries
This example depends on two libraries:
- control_library
- ScopeMimicry
To use them, you have to add the following lines in platformio.ini file:
lib_deps=
control_library = https://github.com/owntech-foundation/control_library.git
scope = https://github.com/owntech-foundation/scopemimicry.git
Define a regulator
The voltage regulation will be done by a proportional resonant regulator.
This component is provided by the OwnTech control library control_lib.
The Proportional Resonant regulator is initialized with the lines above:
The parameters are defined with these values:
static Pr prop_res; // controller instanciation.
static float32_t Kp = 0.02F;
static float32_t Kr = 4000.0F;
static float32_t Ts = control_task_period * 1.0e-6F;
static float32_t w0 = 2.0 * PI * 50.0; // pulsation
static float32_t Udc = 40.0F;
To view some variables.
After stop i.e. in IDLE mode you can retrieve some data by pressing 'r'. It calls a
function dump_scope_datas() which send to the console variables recorded during
the power flow phase.
But before running, you have to add one line in the file platfomio.ini
And you have to put the python script filter_datas_recorded.py in a monitor directory
which must be in you parent project directory. Then the script should capture the
console stream to put it in a txt file named year-month-day_hour_minutes_secondes_record.txt.
These files can be plotted using the plot_data.py python script if you have the
matplotlib and numpy modules installed.
Link between voltage reference and duty cycles.
The voltage source is defined by the voltage difference: \(U_{12} = V_{1low} - V_{2low}\).
Link with the duty cycle:
- The leg1 is fixed in buck mode then: \(V_{1low} = \alpha_1 . U_{DC}\)
- The leg2 is fixed in boost mode then: \(V_{2low} = (1-\alpha_2) . U_{DC}\)
We change at the same time \(\alpha_1\) and \(\alpha_2\), then we have : \(\alpha_1 = \alpha_2 = \alpha\).
And then: \(U_{12} = (2.\alpha - 1).U_{DC}\)
\(\alpha = \dfrac{U_{12}}{2.U_{DC}} + 0.5\)